Posted by :
ss
Friday, February 5
Polish notation
The grate polish mathematician came up with a new technique for representation and calculation of arithmetic expression where operator will be before or after the operand called polish notation.Normal expression A+B
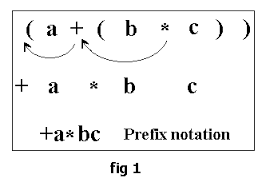
Prefix +AB
Postfix AB+
Infix A+N
Example questions --
convert the following expression to prefix & postfix{[(A+B)/C] *(D-E)}
 Prefix
Prefix
We have to solve above expression according to the priory of operatorsFirst we solve the brackets
={[(+AB)/C]*(-DE)}
={[/+ABC]*(-DE)}
={*/+ABC-DE}
Prefix expression is */+ABC-DE
Postfix
={[(AB+)/C]*(DE-)}
={[AB+C/]*(DE-)}
={AB+CD/DE-*}
=AB+CD/DE-*
postfix expression is AB+CD/DE-*
Algorithms for converting infix to postfix using stack
- Add a unique symbol # into stack and add it in the end of array infix. A*(B+C^D)-E^F #
- Scan the symbol of array infix one by one from left to right.
- Symbol is left parenthesis '(' then add it to the array.
- Symbol is operand then add it to array postfix.
- Symbol is operator then pop the operator which have same priority or higher priority then operator which occurred .
- Add the pop operator to array.
- Add the scaned symbole into stack.
- Symbol is right parenthesis ')' then pop all the operator from the stack.
- Symbol is # then pop all the symbol from stack & add them to array except #.
- You ave done it .
For example .
Infix expression is A*(B+C^D)-E^F
A*(B+C^D)-E^F #
| Symbole | Stack | Postfix expression |
| A | A | |
| * | * | A |
| ( | *( | A |
| B | *(+ | AB |
| + | *(+ | AB |
| C | *(+ | ABC |
| ^ | *(+^ | ABC |
| D | *(+^ | ABCD |
| ) | * | ABCD^+ |
| - | - | ABCD^+* |
| E | - | ABCD^+*E |
| ^ | -^ | ABCD^+*E |
| F | -^ | ABCD^+*EF |
| * | -* | ABCD^+*EF^ |
| ( | -*( | ABCD^+*EF^ |
| G | -*( | ABCD^+*EF^G |
| / | -*(/ | ABCD^+*EF^G |
| H | -*(/ | ABCD^+*EF^GH |
| ) | -* | ABCD^+*EF^GH/ |
| # | ABCD^+*EF^GH/*- |
We would like an interactive session. Comment your question below.
Be Updated Be safe !
Cheers !!
Related Posts :
- Back to Home »
- Algorithms , C Programing , Data Structure , Polish Mathematics , postfix & infix expressions , prefix , Stack »
- Polish Mathematics of prefix, postfix , infix expressions & Algorithms










